#激活函数 #深度学习

Activation Function

Requirement要求

• 增加非线性表达 $\Rightarrow$ 使得神经网络可以拟合任意函数
• 连续可导的函数 $\Rightarrow$ 可以使用梯度下降法进行参数更新
• 定义域是 $\mathbb{R}$ $\Rightarrow$ 可以映射所有实数
• 单调递增的函数 $\Rightarrow$ 不改变输入的响应状态

饱和函数

+ Def

$$x\to \mathrm{\infty }{f}^{{}^{\prime }}(x)\to 0$$

• 导致梯度消失
  • 参数不会被更新
• Sigmoid
• Tanh

非饱和函数

• Rectified Linear Unit 修正线性单元 RELU
  • 解决梯度消失问题
• RELU $\to$ Leaky ReLU, Parametric ReLU, ...

Sigmoid

$$\sigma =\frac{1}{1+e^{-y}}{\sigma }^{{}^{\prime }}=\sigma (1-\sigma )$$

---
title: Sigmoid
xLabel: 
yLabel: 
bounds: [-5,5,0,1]
disableZoom: true
grid: true
---
g(x)= 1/(1+E^-x)
f(x)= (1/(1+E^-x))(1-(1/(1+E^-x)))

[!failure]+ Cons

• 非零均值函数

  • 导致参数同时（正向/反向）更新，不利于收敛

• 导数最大值 $\frac{1}{4}$

  • 导致每层梯度被动缩小 4 倍
    • 导致开始的几层梯度几乎不变
      • 就是梯度消失现象 gradient vanishing problem

-

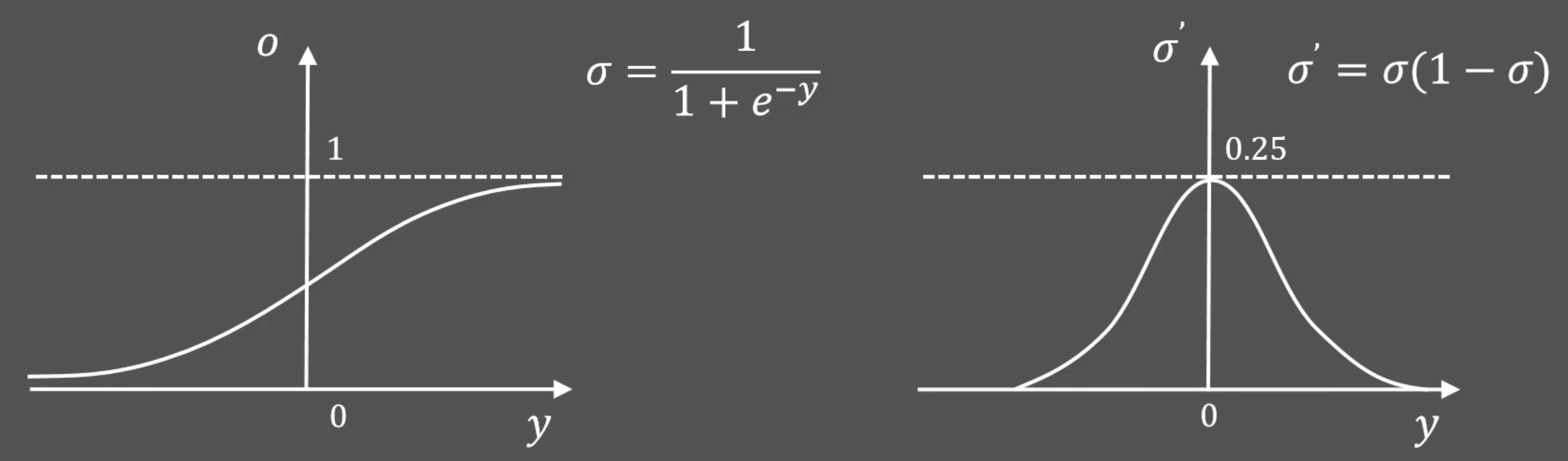
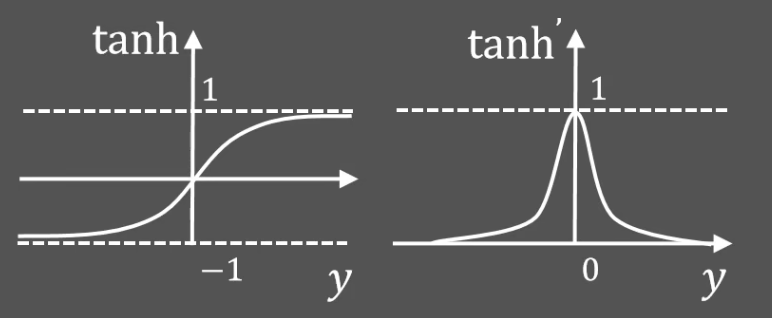
tanh

[!abstract]+

---
title: Derivatives of tanh and tanh
xLabel: 
yLabel: 
bounds: [-10,10,-1,1]
disableZoom: true
grid: true
---
f(x)= (1 - E^-x)/(1 + E^-x)
g(x)= 1 - ((1 - E^-x)/(1 + E^-x))^2

$$\tanh =\frac{1-e^{-y}}{1+e^{-y}}{\tanh }^{{}^{\prime }}=1-{\tanh }^2$$

[!success]+ Pros

• 零均值函数
  • 比 Sigmoid 更快收敛

[!failure]+ Cons

• 饱和函数
  • 梯度消失

-

ReLU (Rectified Linear Unit)

[!abstract]+

$$\text{ReLU}(x)=\{\begin{array}{ll}x,& x>0\\ 0,& x\le 0\end{array}$$

---
title: ReLU
xLabel: 
yLabel: 
bounds: [-2,2,0,2]
disableZoom: true
grid: true
---
f(x) = max(0,x)
g(x) = x>0?1:0

[!success]+ Pros

• 非零均值函数
  • 收敛速度快
• 非饱和函数
  • 避免梯度消失问题